PCA— Basic technique in Machine learning to reduce features with basic Math
Principal component Analysis is the technique used to reduce the dimensions or the columns or the features of a dataset. It also preserves as much information as possible.
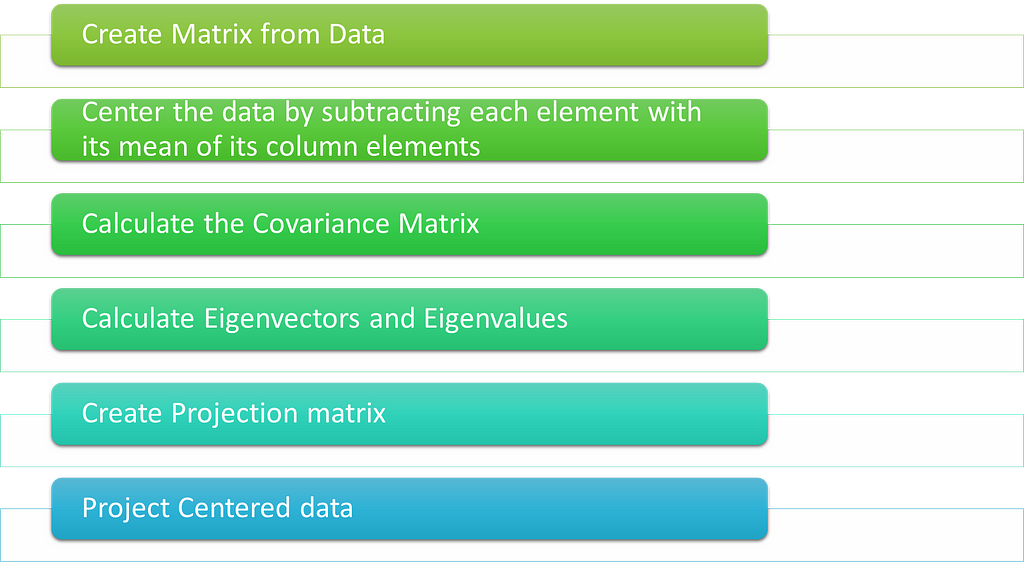
To do this process we should know 3 main concepts
- Eigen Vectors and Eigen Values
- Variance, Covariance and Covariance Matrix
- Projection Matrix with the number of features/columns required.
Let us understand each one of them in detail
Eigen Vectors and Eigen values
Linear Algebra made simple — Eigen Vectors and Eigen Values
Variance, Covariance and Covariance Matrix
Variance — This is simply a measure of how spread out the values are from its mean. For a data set X with n values, the variance is given by
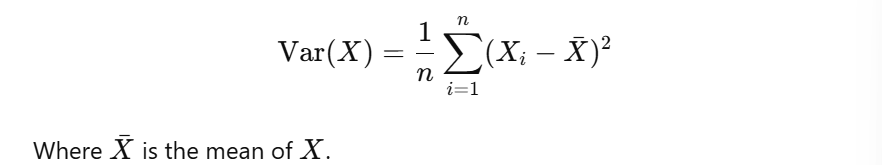
If the variance is large the data points are spread out from the mean
If the variance is small, the data points are close to the mean.
Covariance — Covariance is a measure of how two variables change together. It tell us whether there is a positive or negative linear relationship between two variables.
For two datasets X and Y, the covariance is calculated as:
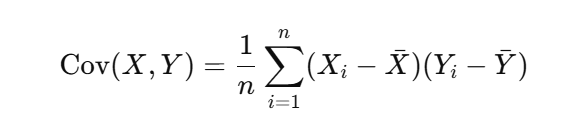
- Positive Covariance means that as X increases, Y tends to increase
- Negative Covariance means that as X increases, Y tends to decrease.
- Zero Covariance means there is no linear relationship between the two variables.
Covariance Matrix — It is a square matrix that shows the covariance between multiple variables.
For Example, X, Y and Z the covariance matrix is
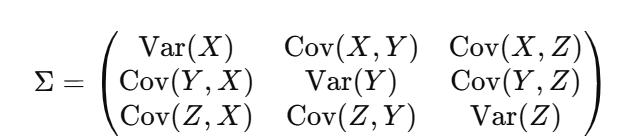
It contains Variances of each variable along the diagonal and Covariances between the pairs of variables on the off-diagonal elements.
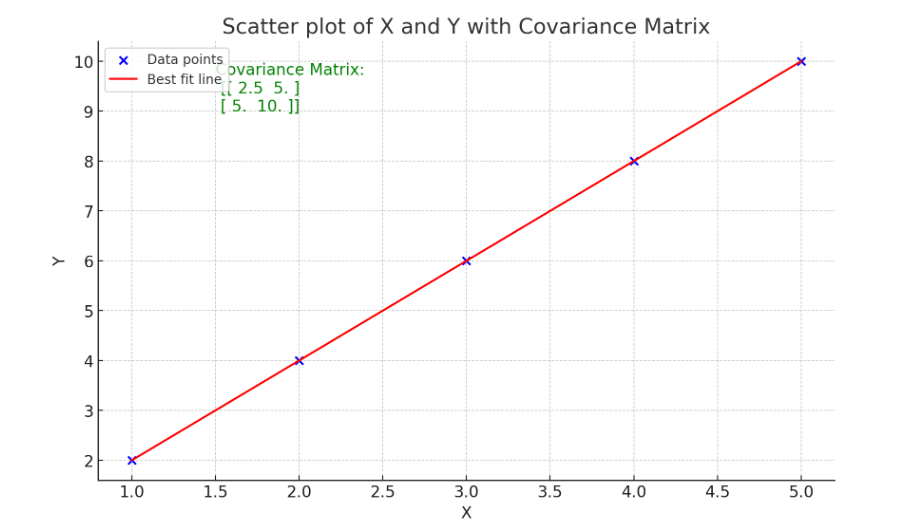
Let’s consider a simple dataset of two variables, X and Y:
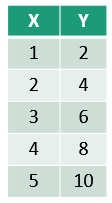
Step 1: Calculate Variance
Mean of X is Xˉ = 3
Mean of Y is Yˉ = 6
Variance of X :
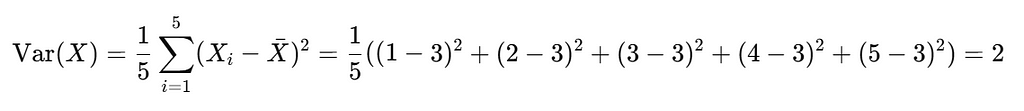
Variance of Y :
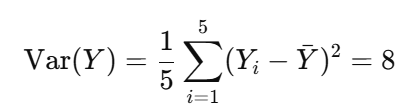
Step 2: Calculate covariance X and Y
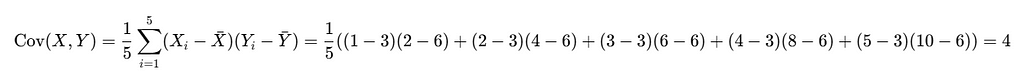
Step 3 : Covariance Matrix
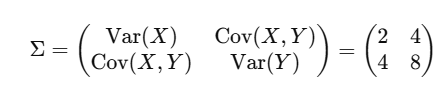
The formula for Covariance matrix in terms of matrices can be given as
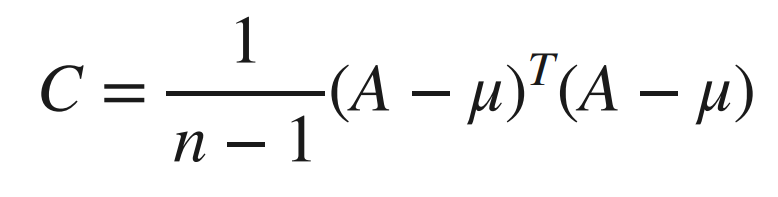
Projection Matrix
Projection is nothing but the shadow of the point in a vector in the other plane or line.
Think of a flashlight shining onto an object. The shadow it casts on a flat surface is the “projection” of the object. In the same way, a projection matrix calculates the shadow (or projection) of a vector onto a lower-dimensional space like a line or plane.
A projection matrix is a mathematical tool used to project a vector onto a subspace (like a line or plane). In simpler terms, it “projects” or “shadows” a vector onto a lower dimension while preserving some geometric properties.
Let’s take an example with vectors in 2D space:
- Suppose you have a vector v, and you want to project it onto another vector a, which lies along a line.
The projection of v onto a is essentially a “shadow” of v on the line defined by a.
If you want to project v onto a, the projection is given by
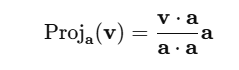
This gives you the vector projection of v onto a. The projection matrix helps automate this process for any vector you want to project onto a subspace.
For any vector a, the projection matrix P that projects any vector onto a is
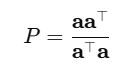
This matrix can be used to project any vector onto the direction of a.
Consider two vectors in 2D space:

Dot Product — v . a
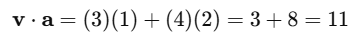
Projection Calculation
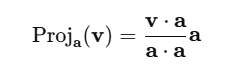
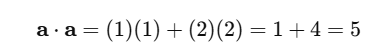
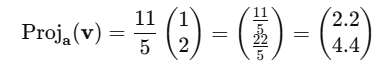
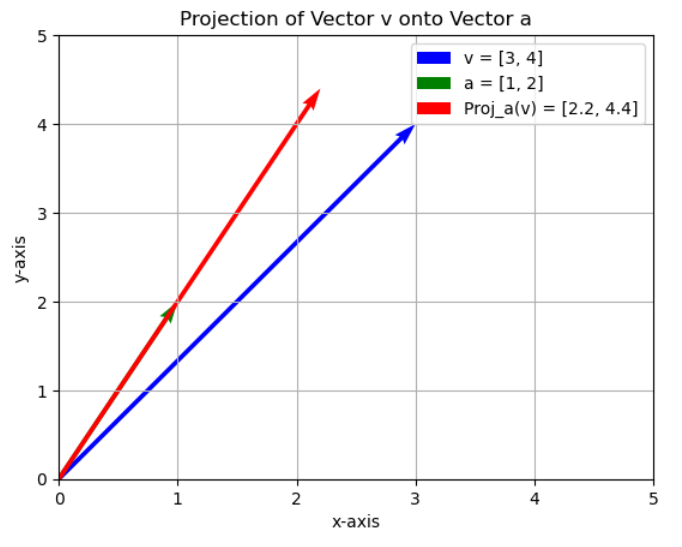
Let us see how it looks on the graph
PCA Analysis
From the above concepts, the number of features can be reduced and projected onto the single space using the steps defined in the first diagram.
