ML Series — Linear Regression-Most used Machine Learning Algorithm: In simple Terms
Linear Regression is the model of supervised machine learning algorithm which is widely used. The concepts used here is referenced as basics for most of the other algorithms.
Let us understand it little deeper with an example. Let us take most commonly used, which is predicting the house prices based on the area of the house in Portland of United States. Here we can draw a graph plotting all the data points which is represented in red dots.
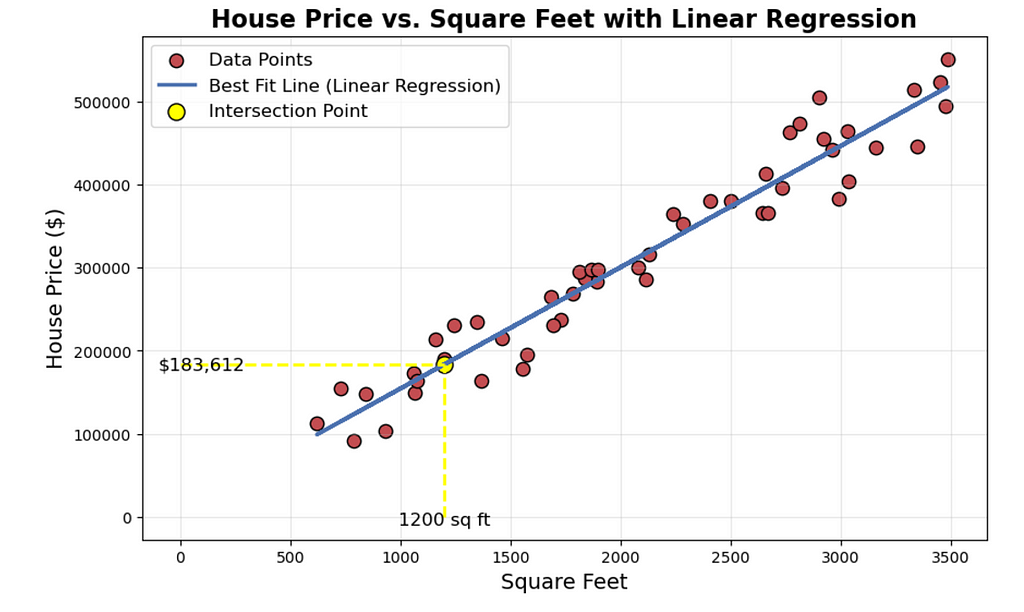
Let us say you are real estate agent and you want to help your clients to sell her house. The dataset here estimates the 1200 sqft house. For this, we build the linear regression model from this dataset. Your model will fit a straight line to the data which looks like the blue line plotted. Based on the straight line fit to the data, you can see that the house is 1200 sq ft, it will intersect the best fit line and if we trace the vertical axis, you can see the price and may be around $180,000. This is the example of supervised learning model.
We call this supervised learning because you are first training a model by giving the data that has right answers and it will predict the prices. This is called regression models because it predicts the numbers like dollars.
Linear regression is one example of a regression model. But there are other model for addressing regression problem too.
In Contrast to the regression model, we have classification model which predicts categories. There are small number of possible outputs. This is called classification problem.
The dataset that we used in the above example to train the linear regression model is called Training Set.
The x ”input” variable is called feature which is size of the house. The y “output” variable is called “target” variable.
We denote 1 single training example (x,y). But if there are multiple data points, we represent them using iwhich is superscript represent the index of the item like 1st data point, 2nd data point, 3 rd data point…

i does not refer to the power but the superscript.
To train the model, you feed the training set, both the input features and output targets to your learning algorithm. Then your supervised algorithm will produce some function. we denote the function as f . f is the model. The job of f is to take the new input x and the output and estimate or a prediction which is called as ŷ which is y-hat. ŷ is the estimation or prediction of y . X is the input or the feature. When the symbol is just the letter y, then that refers to the target, which is the actual true value in the training set. In contrast, y-hat is an estimate. It may or may not be the actual true value.
If you are helping your client to sell the house, the true price is unknown. Your model f predicts the outputs which is estimator and that is the prediction of what the true price will be.

We have predicted the model is a straight line and we do know the equation of straight line as mx + c Here we call it as wx + b where w is the weights and b is the bias. Why Straight line? Linear function is simple and fancy term for straight line instead of some non-linear function like a curve or parabola. Sometimes, we might want to fit more complex non-linear functions as well. But since this linear function is relatively simple and easy to work with, let us use a line as a foundation that will eventually help you to get to more complex models that are non-linear. In this case, we have 1 feature and so this is specifically called Univariate Linear regression. If we have other features that affect the prices of the house like number of bed rooms.
In order for the linear regression to work, we have to construct a cost function. The idea of cost function is one of the most universal and important ideas in machine learning and is used in both linear regression and other most advanced AI models.
What is Cost Function?
Cost function will tell us how well the model is doing so that we can try to get it to do better. As per the description above, we have 2 parameters which is w and b Suppose consider an equation which is f(x) = wx + 1.5When w = 0 then f(x) = 1.5 which is the horizontal line that touches the vertical axis at 1.5. Let us say w = 0.5 and b = 0 then f(x) = 0.5x In this case, when x = 0 then f(x) = 0 and the slope of the line is 0.5.
We have the training set, with linear regression you want to choose values for the parameters w and b so that the straight line you get from the function f somehow fits the data well. The line fits well when the line passes through the data points closer compared to the other lines.
How to find the values of w and b so the prediction y-hat is close to the target y at every value of i?
To do that, we construct the cost function. the cost function takes the prediction y-hat and compares it to the target y by taking y^ — y This difference is called the error which is the measure of how far off to prediction is from the target.
As we would want to get the average of the error for the model predicted, there can be both positive and negative values. so to get uniform error across, we calculate the sum of squares and then find the average value of it. This is called squared error cost function.

This is represented by J(w , b) and the average here is taken as 2m which also gives the same results as dividing by m which is the average. This is used to make it look neater.
In machine learning, different people will use different cost functions for different applications, but the squared error cost function is by far the most commonly used one for linear regression and it gives good results for most of the regression problems.
Our goal is to minimize this J(w , b) which is the cost function.
To get this simplified, let us consider b as 0, which leaves us with f(x) = wx and the cost function is also function of w and not b. Consider w=1 which is constant. in this case the fw(x) would be

What would be the cost function in this case. As you can see y^ which is predicted value is now wx and as w = 1 we get y = x which means the cost function is 0 at every value of x. If we plot the cost function Jw(x) where x axis is w and y-axis is J(w)

Now make the w as 0.5, 0, 1.5, 2 and plot the graph. So how do we choose w is the point where the cost function is at minimum. In this case it is at w = 1 This is how the linear regression use cost function to find the minimum values of J
In the more general case where we had parameters w and b rather than just w, you find the values of w and b that minimize J. As you vary w or vary w and b you end up with different straight lines and when that straight line passes across the data, the cause J is small. The goal of linear regression is to find the parameters w or w and b that results in the smallest possible value for the cost function J. To Summarize,

Consider both the variables w and b then and if both values varies then the graph of the best fit line and cost function looks something like this. Where the cost function looks like the bowl which is the 3 D surface

The same cost function can now be plotted as contour plot which is seen from the above. The minimum point would be the center where the blue is thicker which means it had the overlap of multiple layers.

on choosing different values of w and b we create the line and the line would be the tangent of the curve at that point. The best fit line corresponds to the minimum J value which would be the height of the curve from the base where slope and intercept meets.
So we would need a best algorithm that finds the best fit line with minimum cost function. There is an algorithm for it which is gradient descent. This is one of the most important algorithms in machine learning.
Gradient Descent
Gradient descent is one of the algorithm to find the values of w and b which minimizes the cost function J. This algorithm is widely used in machine learning models. This is used for not only finding the minimum of cost function. In fact, any function can be used in this place to find the minimum.
Suppose you have a complex model where you have w1, w2 …, wn, b where you want to minimize the cost function J. You have to pick the values for w1 through wn and b that gives you smallest possible value of J. We can apply gradient descent to minimize this cost function as well.
Start off with some values of w and b. In linear regression, it wont matter too much of what initial values are. Common choice is to set them both to 0. With gradient descent, we keep changing the values of w and b to reduce J(w, b). There are some more complex functions where they can be more than 1 or more minimum points which is possible in shapes like hammock. For the squared error cost function we always have the bowl shape.

In gradient descent algorithm, we choose the learning rate where it determines how big is the step to evaluate if the point we reached is minimum. If we take bigger steps, we might miss the minimum and if steps are too small, we might reach the minimum point with many iterations which is time taking. So the key here would be choosing the learning rate effectively.
The minimum values are called local minima.
Implementing Gradient Descent

Learning rate is the small positive number which is the small steps.
Partial derivative gives in which direction you would be taking the step with the step size of learning rate. This is because it is the tangent at the point of w which on derivative gives the slope of the tangent line which shows the direction of the minimum.
Similarly, b can be defined as

Sometimes we might be in situation where we should update both w and b simultaneously. In that case, we store the values in temp_w and temp_b and then perform both operations and then store them to w and b. this will eliminate the use of changed value in the b value which is calculated next.
How to choose Learning rate?
What happens if the learning rate is too small, then the derivative is multiplied with the really small rate and so it takes the baby steps to reach the minimum. We need lot of steps to reach there, which is slow.
What happens if the learning rate is too large, the the derivative is multiplied by the large rate which might result in the cost function even bigger than the existing one and we might go further away from the minimum and may not reach it and diverge.
What if you choose a w which is already local minimum. what would be gradient descent. If we draw the tangent, then the slope is parallel to x which means it is 0. then you don’t reduce any value from w and it remains same.
As we approach the minimum, the derivative will approach 0 which means the steps gets smaller and smaller even with the learning rate as fixed rate.
Gradient Descent for Linear Regression
Cost function with square error can never have the multiple local minima and it has one single global minimum.

Consider the f(x) where you want to find the best fit line. Based on the cost function, using the gradient descent, we are finding the minimum value of cost function which is the best fit line.
Happy Learning!!
