Linear Regression — In simple terms for Machine Learning

Linear Regression — In simple terms for Machine Learning

Linear Regression is a supervised machine learning approach, which means you have inputs and outputs of data and you want to find relationship between them

Suppose we have to predict the price of a house based on the size ( In Square feet). Let’s break it down into simpler terms using the housing price example with the equation y = wx + b, where:

• y is the price of the house.
• x is the size of the house (in square feet).
• w is the weight (also known as the slope in linear regression).
• b is the bias (also known as the intercept in linear regression).

Let’s use the values we found:

• w=125 (the amount the price goes up for each additional square foot).
• b=50,000 (the base price when size is zero).

So the equation becomes: Price=125×(Size)+50,000

How It Works:

• Weight (w=125): For every additional square foot, the price of the house goes up by $125. If you increase the size by 10 square feet, the price increases by 125×10=1,250 dollars.
• Bias (b=50,000): This is like the starting point or base price. Even if a house were 0 square feet (which isn’t real, but helps with the math), the base price is $50,000.

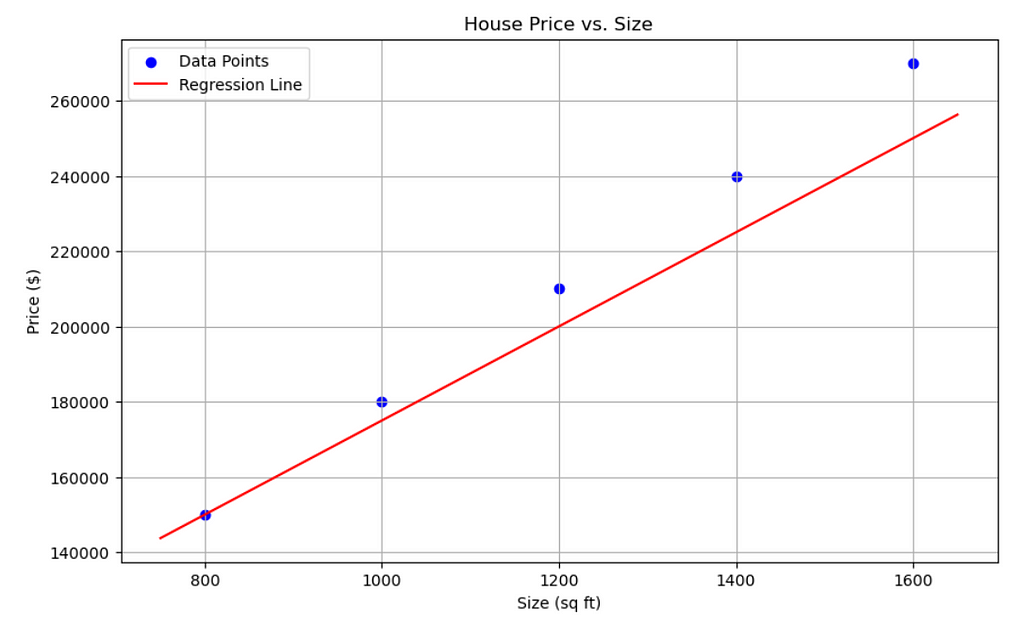
Prediction Example: If you have a house that is 1,200 square feet:

Price = 125×1,200+50,000
Price = 150,000+50,000
Price = 200,000

So, according to this model, a house that is 1,200 square feet should cost $200,000.

In summary, w (weight) tells you how much the price changes with the size, and b (bias) tells you the starting price.

This is good for House price depends on only square feet. But in reality the house price depends on multiple factors like Age of the house and number of bedrooms.

This is called Multiple Linear Regression and here the features are more than one. it is hard to put the features in a single 2D plane. Let us switch to 3D plane where we can represent the different parameters on different axis.

Price = w0 + w1 ×(Size) + w2×(Bedrooms) + w3×(Age)

Where:

• w0 is the bias (intercept) term.
• w1​ is the weight for the size feature.
• w2 is the weight for the number of bedrooms feature.
• w3​ is the weight for the age feature.

Let us interpret with the example

Finding the Weights: Using regression techniques, you determine the values for w0​, w1​, w2 and w3​. Suppose you find:

• w0=30,000 (the base price when all features are zero)
• w1=120 (price increase per square foot)
• w2=10,000 (price increase per bedroom)
• w3=−1,000 (price decrease per year of age)

So the equation becomes: Price=30,000+120×(Size)+10,000×(Bedrooms)−1,000×(Age)

Interpretation:

• Bias (w0=30,000): This is the baseline price when the size, number of bedrooms, and age are zero.
• Weight for Size (w1=120): For each additional square foot, the price increases by $120.
• Weight for Bedrooms (w2=10,000): For each additional bedroom, the price increases by $10,000.
• Weight for Age (w3=−1,000): For each additional year of age, the price decreases by $1,000.

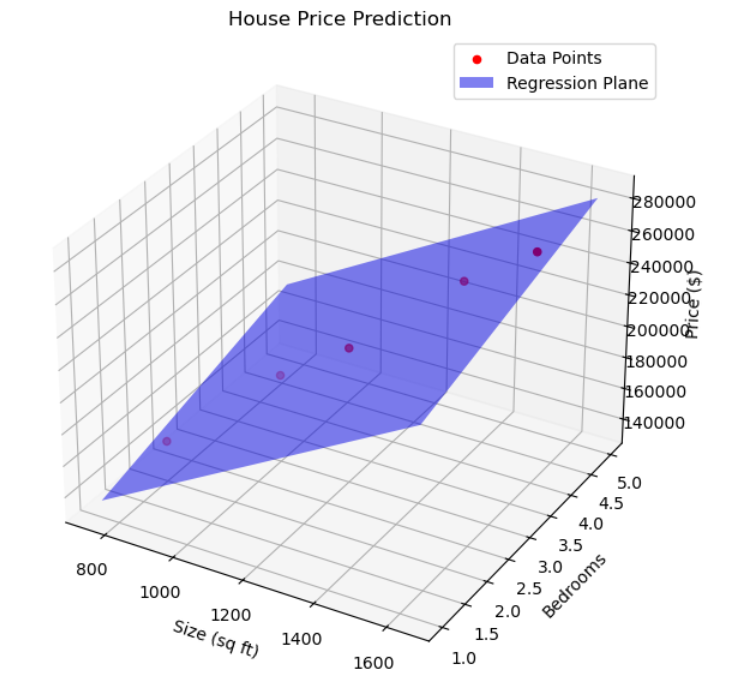
Prediction Example: To predict the price of a house that is:

• 1,200 square feet
• 3 bedrooms
• 5 years old

You use the equation:

Price = 30,000+120×1,200+10,000×3−1,000×5 
Price = 30,000 + 144,000 + 30,000–5,000
Price = 199,000

This article tries to connect the linear regression with the Machine learning which gives an overview. Going further deeper the concepts are little complex but trying to understand it by breaking it into simple and small pieces is the best way to solve complex problems. Hope this example helps to understand the future concepts better.