There are certain conditions associated with the linear regression.
- Linearity
- Nearly normal Residuals
- Constant Variability
Linearity —
Relationship between the explanatory and the response variable should be linear
To check if the linearity is met, we can use the scatterplot of the data or a residuals plot
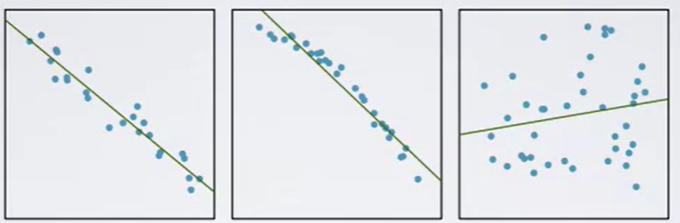

In the above scatterplot and residuals plot of the data points, we see the linear relationship but do not have significant non linear pattern that can be recognized.
Nearly normal residuals —
- Residuals should be normally distributed, centered at 0
- May not be satisfied if there are unusual observations that don’t follow the trend of the rest of the data
- Check using a histogram or normal probability plot of residuals
Constant Variability —
Variability of points around the least squares line should be roughly constant which implies the variability of residuals around the 0 line should be roughly constant as well. This condition is called homoscedasticity.
This is a very good link that shows the variation of Residuals with the regression line — https://gallery.shinyapps.io/slr_diag/
From the above conditions, lets practice the learnt lessons

In the above example, we can see linear trend between our explanatory and our response variable. The residuals plot for this is completely scattered plot. The histograms of the residual plot is centered around 0. the shape of the plot looks fairly symmetric and the normal probability plot with almost all of the dots aligned on straight line, also indicates that the distribution of the residuals is nearly normal.

Just like above, this also has the linear trend, except this time the direction has changed. so we have downward trend between our response and our explanatory variables. The completely random scatter in the residuals plot. A fairly symmetric distribution in the histogram of the residuals and the normal probability looks good.
The above 2 are the happy scenarios where the conditions for linear regression is met. what if the conditions are not met. Let’s look at those examples.

In this case, we have a curved relationship between our explanatory variable and response variable. We see the residual plot is not longer displaying a random scatter around zero. The histogram of the residuals shows a right skew. The same right skew is shown on the normal probability plot as well. So in this case, would it be appropriate to fit a linear model to predict Y from X? Definitely not.

When we look at the curved down relationship, not an extreme curve and it might actually be somewhat difficult to say that it has linear relationship. But look at the residual plot it definitely is curved around the zero and it says the relationship is not linear. The distribution of residuals is no more scatterplot around zero. The histogram of the residual shows a distribution centered at zero, but the distribution does not exactly look very normal. We can also see normal probability plot also shows that the lot of points on the tails actually steer away from normality.
In these 2 examples, the linearity condition has not been met.
What if the constant variability condition has not been met? This usually happens when we have fan shaped model. which means the datapoints are closer at one end and moving further it is distributed across. If the variability is low, the variability of the response variable is low as well.

As X increases the data are fanning out such that the response variable becomes more and more variable. This yields up what we call a fan-shaped residuals plot where we can clearly see that as X increases, the variability of the residuals increase as well. The histogram of the residuals looks fairly symmetric and it’s centered at zero. But looking at the normal probability plot, we can see that we are actually steering a quite a bit away from normality.
