Outliers — The major culprits for deviating the predictions
In a random scattered plot, we calculate the correlation coefficient to get the relationship between explanatory variable and the response variable. What if all the data points are near the regression line which makes the prediction in the right direction but there might be some data points that are way far from the other points and also deviate the prediction.
Outliers are points that fall away from the cloud of points.
There are 2 types of outliers
- Leverage points — Outliers that fall horizontally away from the center of the cloud but don’t influence the slope of the regression line
- Influential points — Outliers that actually influence the slope of the regression line
How to find if it is influential point or not?
To determine if a point is influential, visualize the regression line with and without the point and see if the slope of the line change considerably
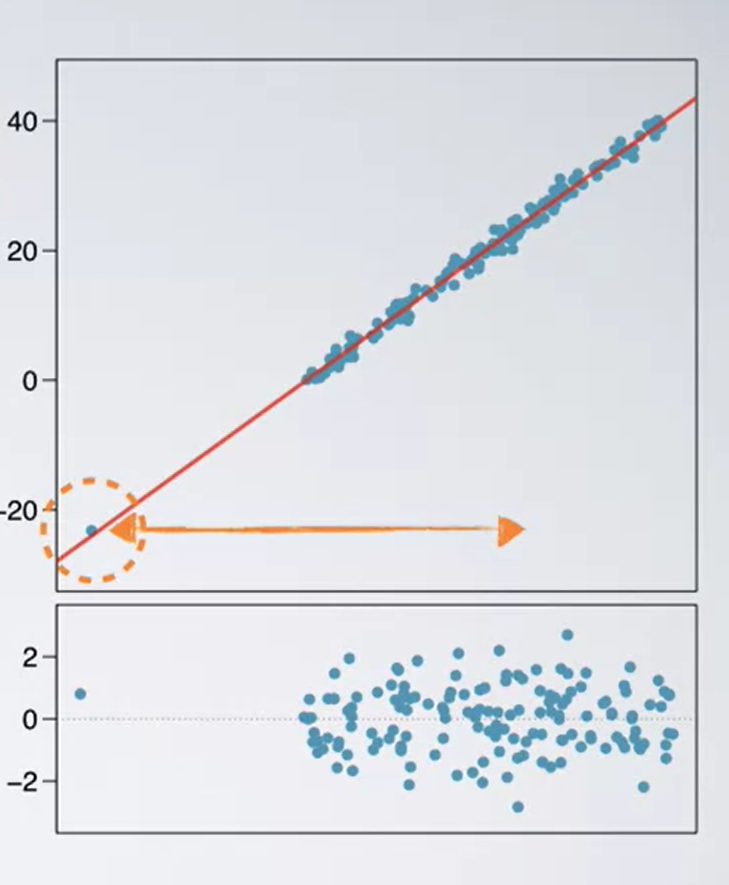
Consider the graph above, there is an outlier here. Can you think which type of outlier is this? Is this influential? What happens to slope if the data point which is the outlier is removed. It appears that the line would say in exactly the same place. So, the outlier point is actually on the trajectory of the regression line. Therefore it does not influence it. This makes this point a leverage point.
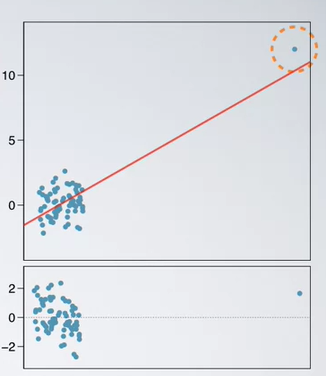
How about this example? The point is outlier and if the point is removed, the line could be a horizantal line and X does not seems to be dependent on Y. The outlier here changes the interpretation of the data. So this is an influential point.
Some point to remember:
- Influential points change the slope (not necessarily the intercept).
- They can reduce R-squared if the remainder of the data show a strong relationship and there is only one or few points that are outside the trajectory of the regression line.
- High leverage points (points farther from the center of the data) are more likely to be influential.
- An influential point does not necessarily change the form of relationship between the variables.
